Envía y clasifica datos de forma eficiente con K-means
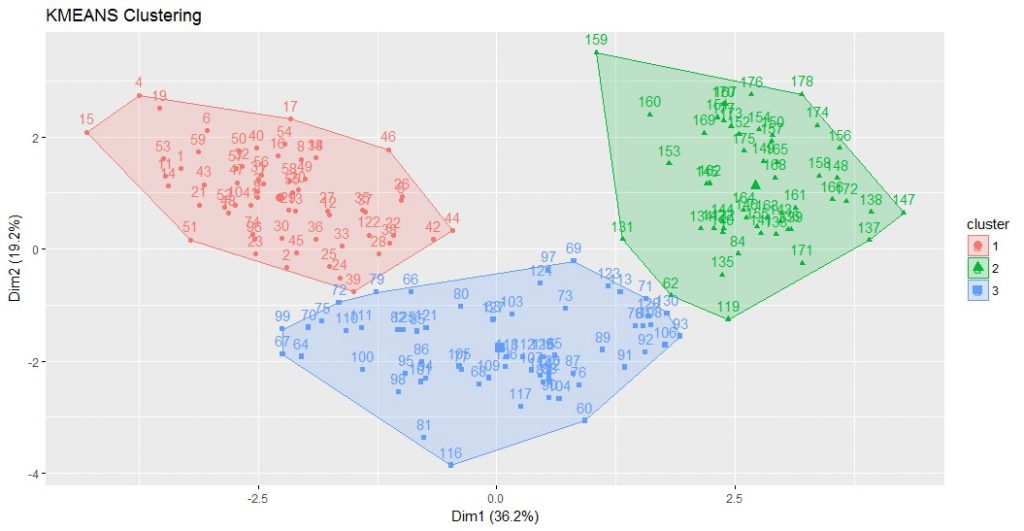
En el mundo de la informática y el análisis de datos, una de las tareas más comunes es la de clasificar grandes cantidades de información. Ya sea para encontrar patrones, segmentar datos o realizar agrupaciones, esta tarea puede resultar ardua y compleja. Es aquí donde entra en juego el algoritmo K-means, una herramienta que permite organizar y clasificar datos de manera eficiente y precisa.
Exploraremos en detalle cómo funciona el algoritmo K-means y cuáles son sus aplicaciones más comunes. Veremos cómo esta técnica puede ayudarnos a encontrar agrupaciones y patrones en grandes conjuntos de datos, y cómo se puede implementar en diferentes lenguajes de programación. Además, conoceremos algunas de sus limitaciones y desafíos, así como sus ventajas y beneficios en comparación con otros algoritmos de clasificación. Prepárate para sumergirte en el fascinante mundo del K-means y descubrir cómo puede optimizar tus análisis de datos.
- Qué es el algoritmo K-means y cómo funciona
- Cuáles son los principales usos del algoritmo K-means en la clasificación de datos
- Cómo se determina el número óptimo de clusters en el algoritmo K-means
- Existen variantes del algoritmo K-means que se adapten a diferentes tipos de datos
- Cuáles son las ventajas y desventajas del algoritmo K-means en comparación con otros algoritmos de clasificación
- Qué técnicas se pueden utilizar para mejorar los resultados del algoritmo K-means
- Cuál es la diferencia entre el algoritmo K-means y otros algoritmos de agrupamiento, como el DBSCAN o el algoritmo de Ward
- Cómo se pueden interpretar los resultados obtenidos a través del algoritmo K-means
- Qué herramientas o bibliotecas de programación se pueden utilizar para implementar el algoritmo K-means
- Cuáles son algunos ejemplos prácticos de aplicaciones del algoritmo K-means en distintas industrias y campos de estudio
- Preguntas frecuentes (FAQ)
Qué es el algoritmo K-means y cómo funciona
El algoritmo K-means es un método de agrupamiento no supervisado que se utiliza para clasificar datos en grupos o clústeres. Su objetivo principal es encontrar patrones y similitudes en los datos sin la necesidad de etiquetas predefinidas. Funciona dividiendo los datos en k grupos diferentes, donde k es un número predefinido por el usuario.
El algoritmo K-means comienza asignando puntos de manera aleatoria a los diferentes grupos y luego calcula el centroide de cada grupo. Luego, asigna cada punto al grupo cuyo centroide esté más cerca. Este proceso continúa iterativamente hasta que los centroides ya no se modifican significativamente o se alcanza un número máximo de iteraciones.
El cálculo de la distancia entre los puntos y los centroides se realiza utilizando una métrica como la distancia euclidiana. Una vez que los datos se han clasificado en grupos, se pueden tomar decisiones y extraer información valiosa a partir de ellos.
Cuáles son los principales usos del algoritmo K-means en la clasificación de datos
El algoritmo K-means es ampliamente utilizado en la clasificación de datos debido a su eficiencia y simplicidad. Se utiliza en una variedad de aplicaciones donde es necesario agrupar elementos similares en conjunto. Algunos de los principales usos de K-means incluyen la segmentación de clientes en base a sus preferencias de compra, la clasificación de documentos en categorías temáticas y la agrupación de imágenes por su contenido visual.
La principal ventaja de K-means es su capacidad para manejar grandes volúmenes de datos de manera eficiente. El algoritmo calcula iterativamente los centroides de los grupos, minimizando la distancia entre los puntos de datos y sus centroides correspondientes. Esto permite una rápida asignación de puntos de datos a grupos, lo que es especialmente útil cuando se trabaja con conjuntos de datos masivos.
Otro uso común de K-means es en la compresión de datos. El algoritmo puede agrupar puntos de datos similares en un solo representante, lo que reduce la cantidad de almacenamiento necesaria para guardar la información. Esto es especialmente útil en aplicaciones donde el espacio de almacenamiento es limitado, como la transmisión de datos a través de redes.
El algoritmo K-means es una herramienta poderosa y versátil en la clasificación de datos. Su capacidad para manejar grandes volúmenes de datos de manera eficiente y su facilidad de implementación lo convierten en una opción popular en una variedad de aplicaciones. Ya sea para segmentar clientes, clasificar documentos o comprimir datos, K-means es una elección confiable para enviar y clasificar datos de forma eficiente.
Cómo se determina el número óptimo de clusters en el algoritmo K-means
El algoritmo K-means es ampliamente utilizado para la agrupación de datos en el campo de la minería de datos y el aprendizaje automático. Sin embargo, una de las preguntas más frecuentes que surgen al utilizar este algoritmo es cómo determinar el número óptimo de clusters. Esta pregunta es crucial ya que el número de clusters afecta directamente la efectividad de la clasificación y la interpretación de los resultados.
Existen diferentes métodos para determinar el número óptimo de clusters en el algoritmo K-means. Uno de los enfoques más comunes es el llamado "método del codo". Este método implica realizar una serie de ejecuciones del algoritmo K-means para diferentes valores de k (el número de clusters) y luego trazar la suma de las distancias al cuadrado de cada punto al centroide más cercano en función de k.
El objetivo es encontrar el punto en el gráfico donde la disminución en la suma de las distancias al cuadrado se desacelera significativamente, formando una especie de "codo". Este punto indica el número óptimo de clusters, ya que a partir de este punto, agregar más clusters no aporta muchos beneficios en términos de mejora de la agrupación.
Evaluación de la calidad de la agrupación
Otro enfoque para determinar el número óptimo de clusters es evaluar la calidad de la agrupación utilizando medidas como la cohesión y la separación. La cohesión mide cuán similares son los puntos dentro de cada cluster, mientras que la separación mide cuán diferentes son los puntos entre diferentes clusters.
Para calcular la cohesión, se puede utilizar la suma de las distancias al cuadrado de cada punto al centroide de su cluster. Cuanto menor sea esta suma, mayor será la cohesión y mejor será la calidad de la agrupación. Por otro lado, la separación se puede calcular como la suma de las distancias al cuadrado entre los centroides de cada cluster. Cuanto mayor sea esta suma, mayor será la separación y mejor será la calidad de la agrupación.
Al evaluar la calidad de la agrupación para diferentes valores de k, se puede observar cómo estas medidas varían y seleccionar el número óptimo de clusters en función de qué valor de k maximiza la cohesión y minimiza la separación.
Validación cruzada
Otro método utilizado para determinar el número óptimo de clusters en el algoritmo K-means es la validación cruzada. Este enfoque implica dividir el conjunto de datos en diferentes subconjuntos y realizar múltiples ejecuciones del algoritmo K-means para cada subconjunto con diferentes valores de k.
Luego, se pueden utilizar medidas como el índice de silueta o la suma de las distancias al cuadrado para evaluar la calidad de la agrupación para cada valor de k en cada subconjunto. Se selecciona el valor de k que obtiene los mejores resultados en términos de estas medidas en promedio a través de los diferentes subconjuntos.
La validación cruzada permite tener una visión más robusta de la calidad de la agrupación y evitar la elección de un número óptimo de clusters que esté sesgado por un subconjunto particular de datos.
Análisis de dominio
Además de los métodos mencionados anteriormente, también se puede realizar un análisis de dominio para determinar el número óptimo de clusters en el algoritmo K-means. Este enfoque implica utilizar el conocimiento experto en el campo de estudio o la naturaleza de los datos para seleccionar un valor de k adecuado.
Por ejemplo, en el campo de la genética, se puede utilizar el número de grupos conocidos de especies o linajes genéticos para determinar el número óptimo de clusters. En el campo de la geología, se puede utilizar la estructura geológica conocida para determinar el número óptimo de clusters.
Este enfoque es especialmente útil cuando los métodos anteriores no son concluyentes o cuando se dispone de un conocimiento experto sólido sobre el dominio de estudio.
Existen variantes del algoritmo K-means que se adapten a diferentes tipos de datos
El algoritmo K-means es ampliamente utilizado para clasificar datos en diferentes áreas, como la minería de datos, la inteligencia artificial y la estadística. Sin embargo, existen variantes de este algoritmo que se adaptan mejor a diferentes tipos de datos.
Una de las variantes más comunes es el K-means++ que mejora el rendimiento del algoritmo inicializando los centroides de manera más inteligente. En lugar de seleccionarlos de forma aleatoria, el K-means++ utiliza un esquema de inicialización basado en la distancia entre los puntos de datos, lo que garantiza una mejor convergencia y resultados más estables.
Otra variante es el K-means paralelo, que permite procesar grandes volúmenes de datos con mayor eficiencia
Para aplicaciones que manejan grandes conjuntos de datos, el K-means paralelo es una opción ideal. Este algoritmo utiliza técnicas de paralelización para dividir la carga de trabajo entre múltiples procesadores o máquinas, lo que permite una clasificación más rápida y eficiente.
Además, el K-means paralelo también puede aprovechar la arquitectura de computación en la nube, distribuyendo el procesamiento en múltiples nodos, lo que aumenta aún más la escalabilidad y la capacidad de manejar grandes volúmenes de datos.
El K-means probabilístico es adecuado para datos con incertidumbre o ruido
Cuando los datos son inciertos o contienen ruido, el K-means probabilístico es una opción recomendada. Esta variante utiliza un enfoque de modelado probabilístico que permite asignar probabilidades a la pertenencia de cada punto de datos a un cluster determinado.
El K-means probabilístico es útil en áreas como la genómica, donde los datos pueden ser complejos y ruidosos, y se requiere una clasificación robusta que tenga en cuenta la incertidumbre inherente.
El K-means kernelizado permite la clasificación en espacios de alta dimensionalidad
Cuando los datos se representan en espacios de alta dimensionalidad, como en la clasificación de imágenes o texto, el K-means kernelizado es una elección acertada. Este enfoque utiliza una técnica llamada kernelización para mapear los datos a un espacio de características más alto, donde la separación entre clusters es más clara.
El K-means kernelizado utiliza funciones kernel, como el kernel gaussiano o el kernel lineal, para realizar esta transformación de datos. Esto permite una mejor clasificación y agrupamiento en espacios de alta dimensionalidad, donde los métodos tradicionales pueden ser menos eficientes.
- El algoritmo K-means tiene varias variantes adaptadas a diferentes necesidades de clasificación de datos. El K-means++, el K-means paralelo, el K-means probabilístico y el K-means kernelizado.
Cuáles son las ventajas y desventajas del algoritmo K-means en comparación con otros algoritmos de clasificación
El algoritmo K-means es ampliamente utilizado en el campo de la minería de datos y la clasificación. Tiene varias ventajas y desventajas en comparación con otros algoritmos de clasificación.
Ventajas del algoritmo K-means:
- Es fácil de implementar y entender.
- Es eficiente en términos de tiempo de ejecución, especialmente para conjuntos de datos grandes.
- Puede manejar datos numéricos y categóricos.
- Es escalable y puede manejar grandes conjuntos de datos sin problemas.
- Puede trabajar con cualquier número de clusters predefinidos.
- Es adecuado para la clasificación de grandes volúmenes de datos en tiempo real.
Desventajas del algoritmo K-means:
- Es sensible a los valores iniciales de los centroides, lo que puede llevar a resultados diferentes en cada ejecución.
- No es adecuado para datos con formas no esféricas o con tamaños de cluster desiguales.
- Es sensible a los valores atípicos y puede verse afectado por ellos.
- La elección incorrecta del número de clusters puede llevar a resultados inadecuados.
- El algoritmo puede converger a un óptimo local en lugar del óptimo global.
A pesar de sus limitaciones, el algoritmo K-means sigue siendo ampliamente utilizado debido a su simplicidad y eficiencia en muchos escenarios de clasificación. Sin embargo, es importante tener en cuenta sus ventajas y desventajas al elegirlo como algoritmo de clasificación en un proyecto específico.
Qué técnicas se pueden utilizar para mejorar los resultados del algoritmo K-means
El algoritmo K-means es ampliamente utilizado para la clasificación y agrupación de datos en diversas aplicaciones. Sin embargo, en ocasiones, los resultados obtenidos pueden no ser óptimos y es necesario aplicar técnicas adicionales para mejorar su eficiencia.
1. Inicialización inteligente de centroides
Una de las técnicas más comunes para mejorar los resultados del algoritmo K-means es utilizar una inicialización inteligente de los centroides. En lugar de seleccionarlos al azar, se pueden utilizar técnicas como K-means++ que aseguran que los centroides iniciales estén alejados unos de otros, lo que puede conducir a una mejor convergencia.
2. Normalización de variables
La normalización de variables es otra técnica que puede mejorar los resultados de K-means. Al normalizar las variables, se asegura que todas tengan la misma escala, evitando así que variables con valores más grandes dominen el proceso de agrupamiento.
3. Selección adecuada de número de clusters
El número de clusters es un parámetro crítico en el algoritmo K-means. Una selección incorrecta puede llevar a resultados no deseables. Para abordar este problema, se pueden utilizar técnicas como el método del codo o el coeficiente de silueta para encontrar el número óptimo de clusters.
4. Uso de técnicas de clustering jerárquico
Otra técnica que puede mejorar los resultados de K-means es combinarlo con técnicas de clustering jerárquico. Estas técnicas permiten capturar estructuras de agrupamiento a diferentes niveles y proporcionan una visión más completa de los datos.
5. Aplicación de K-means en múltiples iteraciones
En algunos casos, una única ejecución de K-means puede no ser suficiente para obtener los resultados deseados. Para mejorar la calidad de los clusters, se puede aplicar K-means en múltiples iteraciones, utilizando los centroides finales de una ejecución como puntos iniciales de la siguiente.
6. Evaluación y ajuste de hiperparámetros
Finalmente, es importante evaluar y ajustar los hiperparámetros del algoritmo K-means para obtener mejores resultados. Estos hiperparámetros incluyen el número máximo de iteraciones, el criterio de convergencia y la métrica de distancia utilizada.
El algoritmo K-means puede beneficiarse de diversas técnicas para mejorar la eficiencia y los resultados del proceso de clustering. Desde una inicialización inteligente de centroides hasta la aplicación de K-means en múltiples iteraciones, estas técnicas pueden ayudar a obtener clusters de mayor calidad y a extraer información más precisa de los datos.
Cuál es la diferencia entre el algoritmo K-means y otros algoritmos de agrupamiento, como el DBSCAN o el algoritmo de Ward
El algoritmo K-means es uno de los métodos más populares para el agrupamiento de datos. A diferencia de otros algoritmos como el DBSCAN o el algoritmo de Ward, el K-means se basa en la asignación de cada dato a un determinado número de clusters predefinidos.
El algoritmo K-means utiliza la técnica de clustering duro, lo que significa que cada dato pertenece estrictamente a un solo cluster. Por otro lado, algoritmos como el DBSCAN utilizan la técnica de clustering suave, donde los datos pueden pertenecer a múltiples clusters con diferentes grados de pertenencia.
En cuanto a la eficiencia, el algoritmo K-means es altamente eficiente ya que utiliza una estrategia de búsqueda exhaustiva para encontrar los centroides óptimos de los clusters. Por otro lado, el DBSCAN y el algoritmo de Ward utilizan técnicas más complejas que pueden requerir un mayor tiempo computacional.
La principal diferencia entre el algoritmo K-means y otros algoritmos de agrupamiento radica en la forma en que asignan los datos a los clusters y en su eficiencia computacional. Dependiendo de los requisitos y características de los datos, cada algoritmo puede ser más adecuado que otro.
Cómo se pueden interpretar los resultados obtenidos a través del algoritmo K-means
Una vez que hemos aplicado el algoritmo K-means a nuestros datos, es fundamental poder interpretar los resultados obtenidos. Esto nos permitirá comprender mejor la estructura y los patrones presentes en nuestros datos para así tomar decisiones informadas.
Una forma de interpretar los resultados es analizando los centroides generados por el algoritmo. Un centroide representa el centro de cada cluster y proporciona información sobre las características promedio de los elementos que pertenecen a ese cluster. Por lo tanto, podemos utilizar los centroides para inferir características comunes dentro de cada grupo.
Además de los centroides, también es útil observar la dispersión de los datos dentro de cada cluster. Esto nos dará una idea de qué tan compactos son los grupos. Si encontramos clusters con una alta dispersión, esto podría indicar la presencia de outliers o la existencia de subgrupos dentro de ese cluster.
¿Qué hacer si los resultados obtenidos no son satisfactorios?
En algunos casos, los resultados obtenidos a través del algoritmo K-means pueden no ser completamente satisfactorios. Esto puede ocurrir si los datos no están bien estructurados o si los grupos no son fácilmente separables.
Si nos encontramos en esta situación, existen algunas estrategias que podemos seguir para mejorar los resultados. Una opción es utilizar una variante del algoritmo K-means, como el K-means++ o el Mini-batch K-means, que pueden producir resultados más precisos o más rápidos, respectivamente.
Otra estrategia es preprocesar los datos antes de aplicar el algoritmo. Esto puede implicar normalizar o estandarizar los datos, eliminar outliers o reducir la dimensionalidad mediante técnicas como PCA o t-SNE.
Además, también es importante tener en cuenta el número de clusters que hemos seleccionado inicialmente. Si los resultados no son satisfactorios, podemos probar con diferentes valores de K y evaluar cómo se modifican los resultados. Podemos utilizar métricas como el coeficiente de silueta o la suma de los cuadrados internos para determinar qué valor de K nos proporciona una partición más adecuada.
Interpretar los resultados obtenidos a través del algoritmo K-means implica analizar los centroides y la dispersión de los datos dentro de cada cluster. Si los resultados no son satisfactorios, podemos considerar utilizar variantes del algoritmo, preprocesar los datos o probar con diferentes valores de K.
Qué herramientas o bibliotecas de programación se pueden utilizar para implementar el algoritmo K-means
Existe una amplia variedad de herramientas y bibliotecas de programación que se pueden utilizar para implementar el algoritmo K-means de forma eficiente. Entre las opciones más populares se encuentran:
1. Python
Python es uno de los lenguajes de programación más utilizados para el análisis de datos y la implementación de algoritmos de clasificación. Bibliotecas como Scikit-learn y K-means de NumPy ofrecen funciones y métodos optimizados para la implementación de K-means.
2. R
R es otro lenguaje de programación ampliamente utilizado en el campo del análisis de datos. El paquete "stats" de R incluye una función para implementar el algoritmo K-means de forma sencilla y eficiente.
3. MATLAB
MATLAB es un entorno de programación diseñado específicamente para el procesamiento de señales, imágenes y datos numéricos. Proporciona una función integrada para implementar el algoritmo K-means y realizar análisis de clustering de manera eficiente.
4. Java
Java es un lenguaje de programación versátil que se utiliza ampliamente en el desarrollo de aplicaciones empresariales. Existen diversas bibliotecas de terceros, como ELKI y Weka, que ofrecen implementaciones eficientes del algoritmo K-means.
5. C/C++
C/C++ son lenguajes de programación de bajo nivel que ofrecen un control preciso sobre el rendimiento y la eficiencia. En C++, la biblioteca "OpenCV" ofrece una implementación eficiente del algoritmo K-means para el procesamiento de imágenes y la segmentación de datos.
Hay una amplia gama de herramientas y bibliotecas de programación disponibles para implementar el algoritmo K-means. La elección de la herramienta dependerá del lenguaje de programación preferido y de los requisitos específicos del proyecto.
Cuáles son algunos ejemplos prácticos de aplicaciones del algoritmo K-means en distintas industrias y campos de estudio
El algoritmo K-means es una técnica de aprendizaje no supervisado que se utiliza para agrupar datos en diferentes categorías. Su versatilidad lo ha convertido en una herramienta ampliamente utilizada en diversas industrias y campos de estudio. A continuación, se presentan algunos ejemplos prácticos de cómo se ha implementado el algoritmo K-means en diferentes áreas:
1. Análisis de mercado
En el mundo empresarial, el algoritmo K-means se utiliza para analizar patrones de comportamiento de los clientes y segmentar el mercado en grupos homogéneos. Esto permite a las empresas comprender las preferencias de sus consumidores y adaptar sus estrategias de marketing en consecuencia.
2. Medicina
En medicina, el algoritmo K-means se ha utilizado para clasificar y analizar datos médicos. Por ejemplo, puede ayudar a identificar diferentes subgrupos de pacientes según sus características clínicas y genéticas. Esto permite a los médicos personalizar los tratamientos y mejorar la precisión de los diagnósticos.
3. Análisis de sentimientos
En el campo de la Inteligencia Artificial, el algoritmo K-means se utiliza para analizar el sentimiento de los usuarios en las redes sociales. Puede agrupar los comentarios y opiniones en diferentes categorías, como positivo, negativo o neutral. Esto brinda información valiosa para las empresas que desean comprender la percepción de sus productos o servicios.
4. Procesamiento de imágenes
El algoritmo K-means también se ha utilizado en el procesamiento de imágenes. Puede ayudar a segmentar una imagen en regiones de colores similares, lo cual es útil en aplicaciones como la detección de objetos, la compresión de imágenes y la eliminación de ruido.
5. Bioinformática
En el campo de la bioinformática, el algoritmo K-means se utiliza para analizar grandes conjuntos de datos genéticos y agrupar secuencias de ADN en diferentes categorías. Esto permite a los investigadores identificar patrones genéticos y comprender mejor la estructura y función de los genes.
El algoritmo K-means tiene aplicaciones prácticas en una amplia gama de industrias y campos de estudio. Su capacidad para clasificar y agrupar datos de manera eficiente lo convierte en una herramienta valiosa para comprender y analizar grandes conjuntos de datos en diversas áreas.
Preguntas frecuentes (FAQ)
1. ¿Qué es K-means?
K-means es un algoritmo de aprendizaje automático no supervisado que se utiliza para clasificar y agrupar datos en clústeres.
2. ¿Cómo funciona el algoritmo K-means?
El algoritmo K-means comienza seleccionando k centroides iniciales y asignando cada dato al centroide más cercano. Luego, los centroides se recalculan en base a los datos asignados y este proceso se repite hasta que los centroides ya no cambien o se alcance un número máximo de iteraciones.
3. ¿Cuáles son las aplicaciones del algoritmo K-means?
K-means se utiliza en diversas aplicaciones, como la segmentación de clientes, la agrupación de noticias o documentos, la clasificación de imágenes y la compresión de datos.
4. ¿Cómo se selecciona el número óptimo de clústeres en K-means?
Para seleccionar el número óptimo de clústeres en K-means, se puede utilizar el método del codo, que consiste en graficar la suma de errores cuadráticos para cada número de clústeres y seleccionar el punto de inflexión donde el cambio en la suma de errores cuadráticos se vuelve menos significativo.
5. ¿Cuáles son las limitaciones del algoritmo K-means?
El algoritmo K-means puede verse afectado por la inicialización de los centroides, por lo que puede llegar a converger a mínimos locales en lugar del óptimo global. Además, es sensible a los valores atípicos y no funciona bien con datos de dimensiones altas o no lineales.
Deja una respuesta