Calcula la correlación de variables enviadas en R: guía paso a paso

En el campo de la estadística y el análisis de datos, la correlación juega un papel fundamental para comprender las relaciones entre diferentes variables. La correlación nos permite medir la fuerza y la dirección de la relación entre dos variables, lo que puede ser de gran utilidad en la toma de decisiones y la construcción de modelos predictivos. Una de las herramientas más utilizadas para calcular la correlación es el software R, que proporciona diversas funciones y métodos estadísticos para este propósito.

Te guiaré paso a paso en el cálculo de la correlación de variables utilizando R. Aprenderemos cómo importar nuestros datos, cómo explorar la relación entre variables y cómo interpretar los resultados obtenidos. Además, también veremos cómo visualizar la correlación utilizando gráficos y cómo realizar pruebas de significancia. Si estás interesado en el análisis de datos y la estadística, este artículo te brindará una sólida base para comenzar a utilizar R en tus proyectos de correlación.

Cuál es la importancia de calcular la correlación entre variables en análisis de datos

Calcular la correlación entre variables es fundamental en el análisis de datos, ya que nos permite evaluar la relación y dependencia que existe entre ellas. Esta información es de vital importancia para comprender cómo una variable puede influir en otra, y nos ayuda a identificar patrones y tendencias en los datos.

La correlación nos permite determinar si existe una relación lineal entre dos variables, es decir, si una variable aumenta o disminuye mientras la otra también lo hace de manera proporcional. Además, nos brinda información acerca de la fuerza y dirección de esta relación, si es positiva (ambas variables aumentan juntas) o negativa (una variable aumenta mientras la otra disminuye).

Conocer la correlación entre variables es esencial en muchas áreas, como la estadística, la economía, la psicología y la investigación científica. Nos ayuda a tomar decisiones informadas y a comprender mejor los fenómenos que estamos estudiando. Además, es una herramienta clave en el desarrollo de modelos predictivos, ya que nos permite determinar qué variables son relevantes para hacer predicciones sobre una variable objetivo.

En el análisis de datos, podemos calcular la correlación entre variables utilizando diferentes métodos, como el coeficiente de correlación de Pearson, el coeficiente de correlación de Spearman o el coeficiente de correlación de Kendall. Estos métodos nos permiten obtener un valor numérico que representa la relación entre las variables, que va desde -1 hasta 1.

Calcular la correlación entre variables es esencial para comprender las relaciones y dependencias entre los datos. Nos ayuda a identificar patrones, determinar la fuerza y dirección de una relación y nos proporciona información valiosa para la toma de decisiones y la construcción de modelos predictivos. En la siguiente sección, te explicaré paso a paso cómo calcular la correlación entre variables en el lenguaje de programación R.

Cuáles son las diferentes técnicas de cálculo de correlación utilizadas en estadística

En el campo de la estadística, el cálculo de correlación es una técnica esencial para analizar la relación entre variables. Existen diversas técnicas de cálculo de correlación que se utilizan en diferentes contextos y situaciones. A continuación, te presentaremos algunas de las más comunes:

Correlación de Pearson

La correlación de Pearson es una medida estadística utilizada para medir la relación lineal entre dos variables continuas. Esta técnica calcula el coeficiente de correlación de Pearson, que varía desde -1 hasta 1. Un valor cercano a 1 indica una correlación positiva fuerte, mientras que un valor cercano a -1 indica una correlación negativa fuerte. Un valor de 0 indica que no hay correlación lineal entre las variables.

Correlación de Spearman

A diferencia de la correlación de Pearson, la correlación de Spearman se utiliza para medir la relación entre dos variables ordenadas o variables no paramétricas. Esta técnica se basa en los rangos de las variables y no en los valores exactos. Al igual que la correlación de Pearson, el coeficiente de correlación de Spearman varía desde -1 hasta 1.

Correlación de Kendall

La correlación de Kendall es otra técnica utilizada para medir la relación entre dos variables ordenadas. A diferencia de la correlación de Spearman, la correlación de Kendall no asume una relación lineal. En cambio, se basa en la concordancia y discordancia entre los pares de observaciones. El coeficiente de correlación de Kendall también varía desde -1 hasta 1.

Correlación de punto biserial

La correlación de punto biserial se utiliza para medir la relación entre una variable continua y una variable binaria. Esta técnica calcula el coeficiente de correlación de punto biserial, que también varía desde -1 hasta 1. Un valor cercano a 1 indica que la variable binaria y la variable continua están positivamente relacionadas, mientras que un valor cercano a -1 indica una relación negativa.

Correlación de phi

La correlación de phi se utiliza para medir la relación entre dos variables binarias. Esta técnica calcula el coeficiente de correlación de phi, que también varía desde -1 hasta 1. Un valor cercano a 1 indica una correlación positiva fuerte, mientras que un valor cercano a -1 indica una correlación negativa fuerte. Un valor de 0 indica que no hay correlación entre las variables binarias.

Estas son solo algunas de las técnicas de cálculo de correlación utilizadas en estadística. Cada una de ellas tiene sus propias ventajas y desventajas, y la elección de la técnica adecuada dependerá del tipo de datos y del objetivo del análisis.

Cómo se interpreta el coeficiente de correlación en el análisis de datos

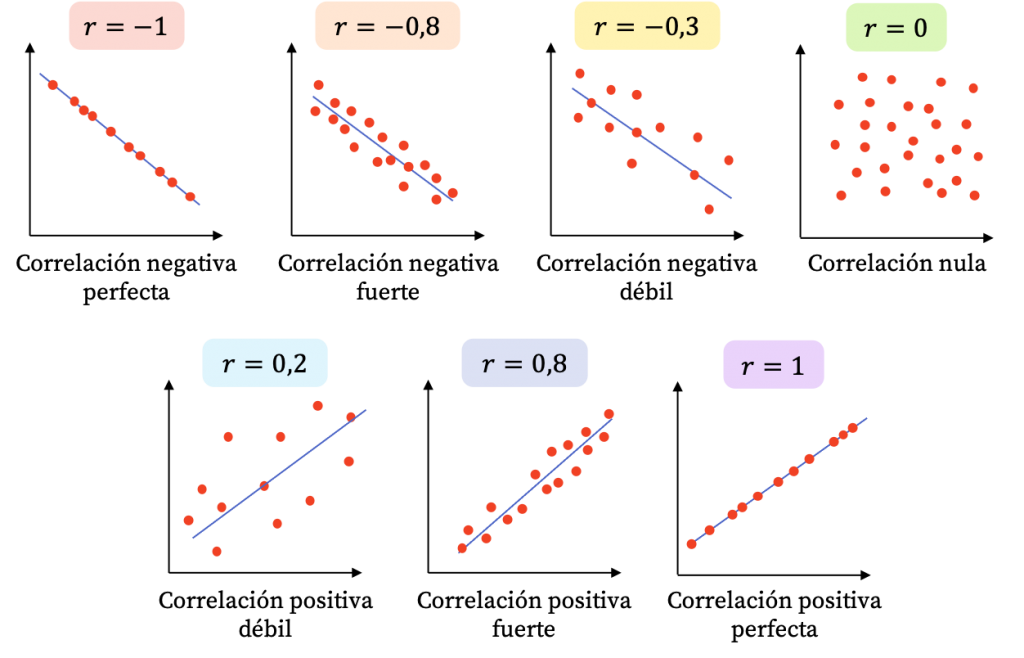
El coeficiente de correlación es una medida estadística que nos permite evaluar la relación entre dos variables. Este coeficiente varía entre -1 y 1, donde -1 indica una correlación negativa perfecta, 1 indica una correlación positiva perfecta y 0 indica que no existe correlación.

Para interpretar el coeficiente de correlación, debemos tener en cuenta su magnitud y su signo. Si el valor del coeficiente está cerca de -1 o 1, podemos decir que existe una fuerte correlación entre las variables. Por otro lado, si el valor está cerca de 0, se puede decir que no existe una relación lineal entre las variables.

El signo del coeficiente también es importante. Si el signo es positivo, significa que a medida que aumenta una variable, la otra también tiende a aumentar. Por el contrario, si el signo es negativo, significa que a medida que una variable aumenta, la otra tiende a disminuir.

Es importante tener en cuenta que el coeficiente de correlación solo mide la relación lineal entre las variables. No nos dice nada sobre la causalidad de esa relación o si hay otros factores que puedan influir en ella. Además, es posible que exista una correlación no lineal entre las variables, por lo que es importante considerar otras medidas de correlación en esos casos.

Cuáles son las ventajas y limitaciones de utilizar la correlación como medida de relación entre variables

La correlación es una medida estadística utilizada para evaluar la relación entre dos variables. Tiene varias ventajas, siendo una de ellas su capacidad para indicar la fuerza y la dirección de la asociación entre las variables. Además, la correlación permite hacer inferencias sobre las tendencias y los patrones de los datos.

Sin embargo, la correlación también tiene limitaciones. En primer lugar, debemos tener en cuenta que la correlación no implica causalidad. Es decir, aunque dos variables estén correlacionadas, no podemos afirmar que una variable cause o sea causada por la otra. Además, la correlación puede verse afectada por valores extremos, lo que puede distorsionar los resultados. Por otro lado, la correlación solo mide la relación lineal entre las variables, por lo que puede no capturar relaciones no lineales.

La correlación es una herramienta útil para evaluar la relación entre variables, pero es importante interpretarla con cautela y considerar las limitaciones mencionadas.

Cuál es la diferencia entre correlación positiva y correlación negativa

La correlación es una medida estadística que evalúa la relación entre dos variables. Cuando dos variables tienen una relación positiva, significa que a medida que una variable aumenta, la otra también tiende a aumentar. Por otro lado, una correlación negativa indica que a medida que una variable aumenta, la otra tiende a disminuir.

En términos más técnicos, la correlación positiva se representa con un coeficiente de correlación que oscila entre 0 y 1, donde 0 indica que no hay ninguna relación entre las variables y 1 indica una relación perfectamente positiva. Por otro lado, la correlación negativa se representa con un coeficiente que oscila entre 0 y -1, donde 0 indica que no hay relación y -1 indica una relación perfectamente negativa.

Es importante tener en cuenta que la correlación no implica causalidad. Solo porque dos variables estén correlacionadas, no significa que una variable cause el cambio en la otra. La correlación simplemente muestra la relación entre las variables.

Cómo se realiza el cálculo de la correlación en R

El cálculo de la correlación es una herramienta estadística que permite medir la relación entre dos variables. En R, existen diferentes métodos para calcular la correlación, como el coeficiente de correlación de Pearson, el coeficiente de correlación de Spearman y el coeficiente de correlación de Kendall.

Para calcular la correlación entre dos variables en R, se puede utilizar la función cor(). Esta función toma como argumentos las variables que se desean comparar y devuelve el valor de la correlación.

Coeficiente de correlación de Pearson

El coeficiente de correlación de Pearson es una medida de la relación lineal entre dos variables. Toma valores entre -1 y 1, donde -1 indica una correlación negativa perfecta, 1 indica una correlación positiva perfecta y 0 indica ausencia de correlación.

Para calcular el coeficiente de correlación de Pearson en R, se puede utilizar el siguiente código:

cor(x, y, method = "pearson")

Donde x y y son las variables que se desean comparar.

Coeficiente de correlación de Spearman

El coeficiente de correlación de Spearman es una medida de la relación monótona entre dos variables. A diferencia del coeficiente de correlación de Pearson, no asume una relación lineal entre las variables.

Para calcular el coeficiente de correlación de Spearman en R, se puede utilizar el siguiente código:

cor(x, y, method = "spearman")

Donde x y y son las variables que se desean comparar.

Coeficiente de correlación de Kendall

El coeficiente de correlación de Kendall es una medida de la relación de concordancia entre dos variables ordinales. Este coeficiente mide la proporción de pares concordantes en relación al total de pares.

Para calcular el coeficiente de correlación de Kendall en R, se puede utilizar el siguiente código:

cor(x, y, method = "kendall")

Donde x y y son las variables que se desean comparar.

El cálculo de la correlación en R es una tarea sencilla que se puede realizar utilizando la función cor(). Dependiendo del tipo de relación entre las variables, se puede utilizar el coeficiente de correlación de Pearson, el coeficiente de correlación de Spearman o el coeficiente de correlación de Kendall.

Cuál es la función más utilizada en R para calcular la correlación entre variables

En R, la función más utilizada para calcular la correlación entre variables es "cor()". Esta función toma como argumento dos vectores numéricos y devuelve el coeficiente de correlación entre ellos. El coeficiente de correlación es un valor que varía entre -1 y 1, y nos indica la fuerza y dirección de la relación entre las variables.

Para calcular la correlación entre dos variables, simplemente necesitamos pasar los dos vectores como argumentos a la función "cor()". Por ejemplo, si tenemos dos vectores llamados "x" y "y", podemos calcular su correlación de la siguiente manera:

correlation <- cor(x, y)

El resultado de este cálculo será almacenado en la variable "correlation". Si queremos mostrar el valor de la correlación en la consola, podemos usar la función "print()":

print(correlation)

Cómo interpretar el resultado de la correlación

Una vez que hemos calculado la correlación entre dos variables en R, es importante interpretar el resultado obtenido. El coeficiente de correlación puede tomar valores entre -1 y 1, y su interpretación varía en función del signo y la magnitud del valor.

Si el coeficiente de correlación es 1, significa que las dos variables tienen una correlación positiva perfecta. Esto quiere decir que cuando una variable aumenta, la otra también lo hace en la misma proporción.

Si el coeficiente de correlación es -1, significa que las dos variables tienen una correlación negativa perfecta. En este caso, cuando una variable aumenta, la otra disminuye en la misma proporción.

Por otro lado, si el coeficiente de correlación es cercano a 0, significa que no existe una relación lineal entre las variables. En este caso, no podemos decir nada acerca de la relación entre las variables basándonos únicamente en el coeficiente de correlación.

Es importante tener en cuenta que el coeficiente de correlación solo mide la relación lineal entre las variables. No nos dice nada acerca de la causalidad o la dirección de la relación. También es importante recordar que el coeficiente de correlación no es una medida de la fuerza o la importancia de la relación, sino simplemente de su magnitud y dirección.

Es posible calcular la correlación entre variables categóricas en R

Existen diversas formas de calcular la correlación entre variables categóricas en R. A continuación, te mostraremos un método paso a paso para realizar este cálculo de manera sencilla y precisa.

Paso 1: Preparación de los datos

Primero, es necesario tener los datos en un formato adecuado. Asegúrate de tener todas las variables que deseas analizar en una matriz de datos, donde cada columna representa una variable.

Puedes utilizar la función as.matrix() para convertir un dataframe en una matriz, si es necesario. Además, es recomendable asegurarse de que todas las variables categóricas estén codificadas como factores utilizando la función as.factor().

Paso 2: Cálculo de la matriz de correlación

Una vez que los datos estén listos, puedes utilizar la función cor() para calcular la matriz de correlación. Esta función toma como argumento la matriz de datos y devuelve una matriz con los coeficientes de correlación entre todas las variables.

Es importante tener en cuenta que la función cor() solo puede calcular la correlación entre variables numéricas. Para calcular la correlación entre variables categóricas, necesitaremos utilizar otro enfoque.

Paso 3: Transformación de variables categóricas en numéricas

Para calcular la correlación entre variables categóricas, es necesario transformarlas en variables numéricas. Esto se puede lograr utilizando la función model.matrix().

La función model.matrix() toma como argumento una fórmula que especifica las variables que se desea transformar y devuelve una matriz de diseño que representa las variables categóricas en forma numérica.

Paso 4: Cálculo de la correlación

Una vez que hayas transformado las variables categóricas en numéricas, puedes utilizar la función cor() nuevamente para calcular la correlación entre estas variables. Esta vez, utilizaremos la matriz de diseño resultante en lugar de la matriz de datos original.

La matriz de correlación resultante contendrá los coeficientes de correlación entre las variables categóricas transformadas.

La correlación entre variables categóricas en R puede calcularse siguiendo estos pasos: preparación de los datos, cálculo de la matriz de correlación, transformación de variables categóricas en numéricas y cálculo de la correlación.

Recuerda que este enfoque solo proporciona una medida de la relación lineal entre las variables categóricas transformadas. Otros métodos, como el coeficiente de contingencia o el coeficiente de asociación, pueden ser más apropiados para analizar la relación entre variables categóricas.

Qué hacer en caso de que haya datos faltantes en las variables a correlacionar

En caso de que haya datos faltantes en las variables que deseas correlacionar en R, existen varias opciones que puedes considerar para manejar esta situación. Una opción es eliminar las observaciones con datos faltantes, lo que significa que perderías información valiosa. Otra opción es realizar la correlación solo con las observaciones completas, pero esto también puede sesgar tus resultados si los datos faltantes no son aleatorios.

Una alternativa es imputar los datos faltantes, lo que significa estimar los valores que faltan en base a los valores disponibles. En R, puedes utilizar funciones como "na.omit()" para eliminar las observaciones con datos faltantes, o "na.exclude()" para realizar la correlación con observaciones completas. Si decides imputar los datos faltantes, puedes utilizar funciones como "na.mean()" para reemplazar los datos faltantes con la media de la variable, o "mice()" para realizar imputación múltiple.

Recuerda que la opción que elijas dependerá del contexto y de la naturaleza de tus datos. Es importante tener en cuenta que cualquier método que elijas puede introducir sesgos en tus resultados, por lo que debes interpretar los resultados con precaución y considerar la posibilidad de realizar análisis de sensibilidad para verificar la robustez de tus conclusiones.

Es posible visualizar la correlación entre variables de forma gráfica en R

Una de las ventajas de utilizar R es la posibilidad de visualizar la correlación entre variables de forma gráfica. Esto es especialmente útil cuando se trabaja con conjuntos de datos grandes y se busca comprender la relación entre las diferentes variables. En este artículo, te guiaré paso a paso para calcular la correlación entre variables en R y te mostraré cómo representarla gráficamente. ¡No te lo puedes perder!

Paso 1: Cargar el conjunto de datos

Lo primero que debemos hacer es cargar el conjunto de datos en R. Para ello, puedes utilizar la función `read.csv()` si el conjunto de datos está en formato CSV, o la función correspondiente si está en otro formato. Asegúrate de tener instalado el paquete necesario para leer ese tipo de archivo, de lo contrario deberás instalarlo con `install.packages()`.

Paso 2: Explorar los datos

Una vez que hayas cargado el conjunto de datos, es importante explorarlo para familiarizarte con su estructura. Puedes utilizar la función `head()` para visualizar las primeras filas del conjunto de datos, y `summary()` para obtener un resumen estadístico de las variables. Además, es recomendable comprobar si hay valores faltantes o atípicos que puedan afectar el análisis de correlación.

Paso 3: Calcular la correlación

Para calcular la correlación entre variables en R, utilizaremos la función `cor()`. Esta función toma como argumento el conjunto de datos y devuelve una matriz de correlación. Si solo te interesa calcular la correlación entre dos variables específicas, debes seleccionar esas variables antes de aplicar la función.

```
# Calculando la correlación entre todas las variables
correlacion_total <- cor(datos)

# Calculando la correlación entre variables específicas
correlacion_especifica <- cor(datos$variable1, datos$variable2)
```

Paso 4: Representar la correlación

Una vez que hayas calculado la matriz de correlación, puedes representarla gráficamente para visualizar mejor las relaciones entre las variables. Una forma común de hacerlo es utilizando un gráfico de matriz de correlación, donde cada celda representa la correlación entre dos variables. Puedes utilizar la función `corrplot()` del paquete `corrplot` para crear este tipo de gráfico.

```
# Instalar el paquete corrplot si no está instalado
install.packages("corrplot")

# Cargar el paquete corrplot
library(corrplot)

# Crear el gráfico de matriz de correlación
corrplot(correlacion_total, method = "circle")
```

Además del gráfico de matriz de correlación, hay otras opciones disponibles para representar la correlación, como gráficos de dispersión o diagramas de caja y bigotes. Puedes explorar estas opciones según tus necesidades y preferencias.

Ahora que conoces los pasos necesarios para calcular la correlación entre variables y representarla gráficamente en R, ¡puedes aplicar este conocimiento a tus propios conjuntos de datos! Recuerda que comprender la relación entre variables es fundamental para realizar análisis más profundos y tomar decisiones informadas en cualquier campo.

Cuáles son las mejores prácticas para la interpretación y presentación de los resultados de la correlación en R

La interpretación y presentación de los resultados de la correlación en R es de vital importancia para cualquier análisis estadístico. Aunque R nos brinda herramientas poderosas para calcular la correlación entre variables, es fundamental seguir las mejores prácticas para garantizar una correcta interpretación de los resultados.

1. Comprender el tipo de correlación

Antes de interpretar los resultados de la correlación en R, es esencial comprender qué tipo de correlación se está calculando. R ofrece varias funciones para calcular la correlación, como cor() y cor.test(), que permiten calcular la correlación de Pearson, Spearman y Kendall.

Es importante tener en cuenta que cada tipo de correlación tiene sus propias suposiciones y se utiliza en diferentes escenarios. Por ejemplo, la correlación de Pearson asume una relación lineal entre las variables, mientras que la correlación de Spearman y Kendall son métodos no paramétricos que no requieren suposiciones sobre la distribución de los datos.

2. Evaluar la significancia estadística

Al interpretar los resultados de la correlación en R, es crucial evaluar la significancia estadística de la correlación encontrada. Esto se puede hacer mediante pruebas de hipótesis, como el valor p.

Un valor p menor que un nivel de significancia dado (por ejemplo, 0.05) indica que la correlación encontrada es estadísticamente significativa, lo que sugiere que existe una relación entre las variables. Por otro lado, un valor p mayor que el nivel de significancia indica que la correlación es probablemente al azar y no significativa.

3. Presentar los resultados de manera clara y concisa

Al presentar los resultados de la correlación en R, es importante ser claro y conciso. Puedes utilizar tablas, gráficos o resúmenes descriptivos para mostrar los resultados de manera visualmente atractiva.

Si estás presentando los resultados en un informe o artículo, asegúrate de proporcionar el contexto necesario para que los lectores comprendan los resultados. Explica el significado de la correlación encontrada y cómo se relaciona con el objetivo del estudio.

4. Considerar el tamaño de la muestra

El tamaño de la muestra es otro factor importante a tener en cuenta al interpretar los resultados de la correlación en R. Muestras pequeñas pueden conducir a estimaciones sesgadas de la correlación y dificultar la detección de relaciones verdaderas entre las variables.

Si tienes una muestra pequeña, es posible que desees considerar el uso de técnicas de remuestreo, como el bootstrap, para obtener estimaciones más precisas de la correlación y evaluar la incertidumbre de los resultados.

5. Evaluar la presencia de valores atípicos

Los valores atípicos pueden tener un impacto significativo en los resultados de la correlación en R. Es importante evaluar la presencia de valores atípicos y, si es necesario, considerar su eliminación o transformación antes de calcular la correlación.

La detección de valores atípicos se puede realizar mediante diversas técnicas, como el análisis de gráficos de dispersión, el cálculo de estadísticas descriptivas y pruebas de valores atípicos multivariados.

Seguir las mejores prácticas para la interpretación y presentación de los resultados de la correlación en R es fundamental para garantizar una correcta y precisa interpretación de los datos. Comprender el tipo de correlación, evaluar la significancia estadística, presentar los resultados de manera clara y concisa, considerar el tamaño de la muestra y evaluar la presencia de valores atípicos son algunos de los aspectos clave a tener en cuenta.

Existen paquetes o librerías adicionales en R que faciliten el análisis de correlación de variables

En R, existen varias librerías que facilitan el análisis de correlación de variables. Algunas de las más populares son:

• Corrplot: Esta librería ofrece una variedad de métodos para visualizar la matriz de correlación, incluyendo gráficos de color y diagramas de dispersión.
• Hmisc: Esta librería proporciona funciones avanzadas para el análisis de datos, incluyendo la función rcorr(), que calcula la matriz de correlación y devuelve los p-valores.
• psych: Esta librería es ampliamente utilizada en la psicometría y proporciona funciones para el análisis de correlación y factores.

Estas librerías adicionales pueden ser instaladas fácilmente en R utilizando el comando install.packages(). Una vez instaladas, puedes cargarlas en tu sesión utilizando el comando library().

Instalando y cargando paquetes en R

Para instalar una librería en R, utiliza el siguiente comando:

install.packages("nombre_del_paquete")

Reemplaza "nombre_del_paquete" por el nombre de la librería que deseas instalar.

Una vez que la librería esté instalada, puedes cargarla en tu sesión de R con el siguiente comando:

library(nombre_del_paquete)

Reemplaza "nombre_del_paquete" por el nombre de la librería que deseas cargar.

Una vez que hayas instalado y cargado las librerías adicionales, estás listo para calcular la correlación de variables en R.

Cuáles son los pasos recomendados para realizar un análisis de correlación completo en R

Para realizar un análisis de correlación completo en R, es importante seguir una serie de pasos que nos asegurarán obtener resultados precisos y confiables. A continuación, te presentamos una guía paso a paso para calcular la correlación de variables en R.

Paso 1: Importar los datos

El primer paso consiste en importar los datos que deseamos analizar. Podemos cargar los datos desde un archivo CSV, Excel u otro formato compatible con R. Utilizaremos la función read.csv() para cargar los datos en un nuevo objeto.

Paso 2: Explorar los datos

Antes de calcular la correlación, es importante explorar los datos para obtener una comprensión completa de las variables. Podemos utilizar las funciones como summary() y str() para obtener estadísticas descriptivas y conocer la estructura de los datos.

Paso 3: Eliminar valores faltantes

Es común que los datos contengan valores faltantes, lo cual puede afectar el cálculo de la correlación. Antes de continuar, es recomendable eliminar los valores faltantes utilizando la función na.omit() para mantener la integridad de los datos.

Paso 4: Calcular la correlación

Una vez que hemos preparado los datos, podemos calcular la correlación entre las variables. Utilizaremos la función cor() para obtener una matriz de correlación que muestra la relación entre todas las variables. Por defecto, se utilizará el coeficiente de correlación de Pearson.

Paso 5: Visualizar la correlación

Es útil visualizar la correlación para obtener una comprensión más clara de las relaciones entre las variables. Podemos utilizar gráficos de dispersión o mapas de calor para representar la correlación. R ofrece una amplia gama de paquetes y funciones para visualizar la correlación.

Paso 6: Interpretar los resultados

Una vez que hemos calculado y visualizado la correlación, es importante interpretar los resultados obtenidos. Podemos examinar los valores de correlación para identificar las relaciones fuertes o débiles entre las variables. También podemos realizar pruebas de significancia para determinar si las correlaciones son estadísticamente significativas.

Paso 7: Conclusiones

Finalmente, podemos concluir nuestro análisis de correlación resumiendo los hallazgos más importantes. Podemos destacar las relaciones más relevantes entre variables y proporcionar recomendaciones basadas en los resultados obtenidos.

Realizar un análisis de correlación en R requiere seguir una serie de pasos que incluyen la importación de datos, exploración de datos, cálculo de correlación, visualización de correlación, interpretación de resultados y conclusiones. Siguiendo esta guía paso a paso, podrás realizar un análisis de correlación completo y obtener información valiosa sobre las relaciones entre variables.

Es la correlación suficiente para determinar la existencia de una relación causal entre variables

La correlación es una herramienta útil para medir la relación entre variables, pero no es suficiente para determinar una relación causal. Una correlación positiva o negativa entre dos variables indica que hay una asociación estadística entre ellas, pero no establece que una variable sea la causa de la otra.

Para establecer una relación causal, se necesita realizar un análisis más profundo que tenga en cuenta otros factores, como los experimentos controlados y la revisión de la literatura existente. Esto es especialmente importante en el campo de las ciencias sociales, donde las variables son extremadamente complejas y están influenciadas por múltiples factores.

La correlación puede ser un primer paso importante para identificar patrones y relaciones en los datos, pero debe complementarse con otras técnicas de análisis para obtener conclusiones más sólidas. Estas técnicas pueden incluir análisis de regresión, pruebas de hipótesis y experimentos controlados.

La correlación es una medida útil para evaluar la relación entre variables, pero no se debe utilizar como evidencia suficiente para establecer una relación causal. Es importante considerar otros factores y realizar un análisis más exhaustivo antes de sacar conclusiones definitivas.

Qué otros métodos complementarios pueden utilizarse en conjunto con la correlación para un análisis más completo de las variables

Además de la correlación, existen otros métodos complementarios que pueden utilizarse en conjunto para realizar un análisis más completo de las variables en R. Estos métodos permiten obtener información adicional sobre la relación entre las variables, brindando una visión más profunda de los datos.

1. Regresión lineal:

La regresión lineal es una técnica que permite modelar la relación entre una variable dependiente y una o más variables independientes. Esta técnica utiliza la correlación para determinar la fuerza y dirección de la relación entre las variables. A través de la regresión lineal, se pueden obtener coeficientes que indican el impacto que cada variable independiente tiene sobre la variable dependiente.

2. Análisis de componentes principales (PCA):

El análisis de componentes principales (PCA) es una técnica utilizada para reducir la dimensionalidad de un conjunto de datos. A través de este método, se pueden identificar las variables más importantes y las relaciones existentes entre ellas. El PCA utiliza la matriz de correlación para determinar las componentes principales, que son combinaciones lineales de las variables originales.

3. Análisis factorial:

El análisis factorial es una técnica que permite identificar los factores subyacentes que están relacionados con un conjunto de variables observadas. A través de este método, se busca determinar las dimensiones latentes que explican la variabilidad de las variables observadas. La matriz de correlación se utiliza para calcular las cargas factoriales, que indican la relación entre cada variable observada y los factores subyacentes.

4. Análisis de conglomerados:

El análisis de conglomerados, también conocido como clustering, es una técnica utilizada para agrupar observaciones similares en conjuntos compactos. La matriz de correlación se utiliza para determinar la similitud entre las observaciones y construir los grupos. Esta técnica es útil para identificar patrones y segmentar los datos en subconjuntos homogéneos.

La correlación es una medida fundamental para determinar la relación entre variables en un análisis de datos. Sin embargo, para obtener una visión más completa, es recomendable utilizar métodos complementarios como la regresión lineal, el análisis de componentes principales, el análisis factorial y el análisis de conglomerados. Estos métodos permiten explorar diferentes aspectos de las variables y proporcionan una mayor comprensión de los datos.

Preguntas frecuentes (FAQ)

1. ¿Qué es la correlación de variables?

La correlación de variables es una medida estadística que indica la relación entre dos o más variables.

2. ¿Para qué se utiliza la correlación de variables?

La correlación de variables se utiliza para determinar si existe una relación entre dos o más variables y cuán fuerte es esa relación.

3. ¿Qué valores puede tomar la correlación de variables?

La correlación de variables puede tomar valores entre -1 y 1. Un valor de -1 indica una correlación negativa perfecta, un valor de 0 indica ausencia de correlación y un valor de 1 indica una correlación positiva perfecta.

4. ¿Cómo se interpreta la correlación de variables?

Un valor de correlación cercano a 0 indica que no hay una relación lineal entre las variables. Un valor cercano a -1 o 1 indica una relación fuerte y lineal, mientras que un valor cercano a 1 indica una relación inversa.

5. ¿Cómo se calcula la correlación de variables en R?

En R, se puede calcular la correlación de variables utilizando la función cor(). Simplemente se deben especificar las variables a comparar y el método de cálculo de la correlación.